一.简介
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1L1+W2L2+W3L3+…+WnLn),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明霍夫曼树的WPL是最小的。
二.基本术语
1.路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2.结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3.树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
三.构造
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
图解过程:
四.编码
利用哈夫曼树求得的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
用图说明如下: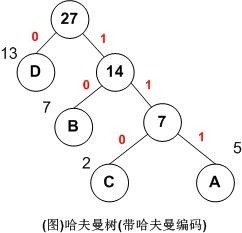
五.例题及代码实现
例:
C++实现:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int ELEMTYPE;
// 哈夫曼树结点结构体
typedef struct HuffmanTree
{
ELEMTYPE weight;
ELEMTYPE id; // id用来主要用以区分权值相同的结点,这里代表了下标
struct HuffmanTree* lchild;
struct HuffmanTree* rchild;
}HuffmanNode;
// 构建哈夫曼树
HuffmanNode* createHuffmanTree(int* a, int n)
{
int i, j;
HuffmanNode **temp, *hufmTree;
temp = malloc(n*sizeof(HuffmanNode));
for (i = 0; i<n; ++i) // 将数组a中的权值赋给结点中的weight
{
temp[i] = (HuffmanNode*)malloc(sizeof(HuffmanNode));
temp[i]->weight = a[i];
temp[i]->id = i;
temp[i]->lchild = temp[i]->rchild = NULL;
}
for (i = 0; i<n - 1; ++i) // 构建哈夫曼树需要n-1合并
{
int small1 = -1, small2; // small1、small2分别作为最小和次小权值的下标
for (j = 0; j<n; ++j) // 先将最小的两个下标赋给small1、small2(注意:对应权值未必最小)
{
if (temp[j] != NULL && small1 == -1)
{
small1 = j;
continue;
}
else if (temp[j] != NULL)
{
small2 = j;
break;
}
}
for (j = small2; j<n; ++j) // 比较权值,挪动small1和small2使之分别成为最小和次小权值的下标
{
if (temp[j] != NULL)
{
if (temp[j]->weight < temp[small1]->weight)
{
small2 = small1;
small1 = j;
}
else if (temp[j]->weight < temp[small2]->weight)
{
small2 = j;
}
}
}
hufmTree = (HuffmanNode*)malloc(sizeof(HuffmanNode));
hufmTree->weight = temp[small1]->weight + temp[small2]->weight;
hufmTree->lchild = temp[small1];
hufmTree->rchild = temp[small2];
temp[small1] = hufmTree;
temp[small2] = NULL;
}
free(temp);
return hufmTree;
}
// 以广义表的形式打印哈夫曼树
void PrintHuffmanTree(HuffmanNode* hufmTree)
{
if (hufmTree)
{
printf("%d", hufmTree->weight);
if (hufmTree->lchild != NULL || hufmTree->rchild != NULL)
{
printf("(");
PrintHuffmanTree(hufmTree->lchild);
printf(",");
PrintHuffmanTree(hufmTree->rchild);
printf(")");
}
}
}
// 递归进行哈夫曼编码
void HuffmanCode(HuffmanNode* hufmTree, int depth) // depth是哈夫曼树的深度
{
static int code[100];
if (hufmTree)
{
if (hufmTree->lchild == NULL && hufmTree->rchild == NULL)
{
printf("id为%d权值为%d的叶子结点的哈夫曼编码为 ", hufmTree->id, hufmTree->weight);
int i;
for (i = 0; i<depth; ++i)
{
printf("%d", code[i]);
}
printf("\n");
}
else
{
code[depth] = 0;
HuffmanCode(hufmTree->lchild, depth + 1);
code[depth] = 1;
HuffmanCode(hufmTree->rchild, depth + 1);
}
}
}
// 哈夫曼解码
void HuffmanDecode(char ch[], HuffmanNode* hufmTree, char string[]) // ch是要解码的01串,string是结点对应的字符
{
int i;
int num[500];
HuffmanNode* tempTree = NULL;
for (i = 0; i<strlen(ch); ++i)
{
if (ch[i] == '0')
num[i] = 0;
else
num[i] = 1;
}
if (hufmTree)
{
i = 0; // 计数已解码01串的长度
while (i<strlen(ch))
{
tempTree = hufmTree;
while (tempTree->lchild != NULL && tempTree->rchild != NULL)
{
if (num[i] == 0)
{
tempTree = tempTree->lchild;
}
else
{
tempTree = tempTree->rchild;
}
++i;
}
printf("%c", string[tempTree->id]); // 输出解码后对应结点的字符
}
}
}
int main()
{
int i, n;
printf("请输入叶子结点的个数:\n");
while (1)
{
scanf("%d", &n);
if (n>1)
break;
else
printf("输入错误,请重新输入n值!");
}
int* arr;
arr = (int*)malloc(n*sizeof(ELEMTYPE));
printf("请输入%d个叶子结点的权值:\n", n);
for (i = 0; i<n; ++i)
{
scanf("%d", &arr[i]);
}
char ch[500], string[500];
printf("请连续输入这%d个叶子结点各自所代表的字符:\n", n);
fflush(stdin); // 强行清除缓存中的数据,也就是上面输入权值结束时的回车符
gets(string);
HuffmanNode* hufmTree = NULL;
hufmTree = createHuffmanTree(arr, n);
printf("此哈夫曼树的广义表形式为:\n");
PrintHuffmanTree(hufmTree);
printf("\n各叶子结点的哈夫曼编码为:\n");
HuffmanCode(hufmTree, 0);
printf("要解码吗?请输入编码:\n");
gets(ch);
printf("解码结果为:\n");
HuffmanDecode(ch, hufmTree, string);
printf("\n");
free(arr);
free(hufmTree);
return 0;
}
结果 :
这里结果只用改一下就好
f}alg55fd5f50f0ddd0d00adafdd5505d50a5{
flag{ddf5dfd0f05550500a5af55dd0d5d0ad}





